import numpy as np
my_string="ATACAA"
my_array=np.array(list(my_string))
print(my_array)['A' 'T' 'A' 'C' 'A' 'A']4 Day3 CNN with DNA sequence
4.1 Objectives
- Developing a CNN Model for classifying sequences
- Example: Developing a model to identify specific DNA motifs bound by an arbitrary transcription factor. The model predicts whether a given transcription factor binds to an input DNA sequence (output: 1) or not (output: 0).”
4.2 Data
To train a deep learning model, labeled data is required (though not always necessary in modern self-supervised learning approaches).
In sequence analysis, DNA sequences paired with their corresponding phenotypes can serve as labeled data (genotype-phenotype paired data).
- For example, to train a deep learning model to predict DNA sequences bound by a specific transcription factor, you would need a dataset containing transcription factor sequence data along with labels indicating whether or not the transcription factor binds to a given DNA sequence (True or False).
Generally, data for statistical analysis is represented as a 2D array, with rows corresponding to samples and columns to variables. In deep learning, data is represented in the same way. The number of samples required depends on the complexity of the model, but typically, at least thousands of samples are needed. Using tens of thousands or more samples is recommended for optimal results.
A dataset collected for deep learning is divided into training and test datasets. Sometimes, the training dataset is further split into training and validation datasets for model development and performance evaluation.
4.2.1 One-hot encoding
For deep learning, data must be represented numerically in a format that machines can process.
One-hot encoding is one of the most widely used methods in deep learning.
For DNA sequences with four types of nucleotides, encoding can be done as follows:
- “A” → [1, 0, 0, 0]
- “T” → [0, 0, 0, 1]
- “G” → [0, 0, 1, 0]
- “C” → [0, 1, 0, 0]
- “A” → [1, 0, 0, 0]
list(my_string)['A', 'T', 'A', 'C', 'A', 'A']np.zeros((7,5))array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])box = np.zeros((3, 7, 5))
type(box)
boxarray([[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]],
[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]],
[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]]])onehot_encode = np.zeros((len(my_array),4), dtype=int)
base_dict = {"A":0, "C":1, "G":2, "T":3}
for i in range(len(my_array)):
onehot_encode[i, base_dict[my_array[i]]] = 1
print(onehot_encode)
print(onehot_encode.shape)[[1 0 0 0]
[0 0 0 1]
[1 0 0 0]
[0 1 0 0]
[1 0 0 0]
[1 0 0 0]]
(6, 4)4.2.2 Set sequence motif for simulation
- Understanding the concepts of PFM (Position Frequency Matrix) and PWM (Position Weight Matrix) is essential.
- Assuming an alignment of several sequences, the PFM represents the frequency of each nucleotide (A, T, G, C) at specific positions in the sequences, while the PWM represents the proportion of each nucleotide at those positions.
from Bio import motifs
from Bio.Seq import Seq
instances = [Seq("TACAA"), Seq("TACGA"), Seq("TACAA")]
m = motifs.create(instances)
pfm = m.counts
print(pfm)
pwm = m.counts.normalize(pseudocounts=0.5)
print (pwm) 0 1 2 3 4
A: 0.00 3.00 0.00 2.00 3.00
C: 0.00 0.00 3.00 0.00 0.00
G: 0.00 0.00 0.00 1.00 0.00
T: 3.00 0.00 0.00 0.00 0.00
0 1 2 3 4
A: 0.10 0.70 0.10 0.50 0.70
C: 0.10 0.10 0.70 0.10 0.10
G: 0.10 0.10 0.10 0.30 0.10
T: 0.70 0.10 0.10 0.10 0.10
- Pseudocounts are used in calculations to avoid division by NULL or zero.
- The PWM (Position Weight Matrix) of a specific sequence motif can be used to search for the motif’s location in a new sequence provided in one-hot encoding format.
- Using a sliding window approach, the motif can be scanned from the beginning to the end of the sequence to identify its presence.
- The following demonstrates how to detect the presence of a given PWM motif (assuming a binary 0 and 1 representation) in a sequence.
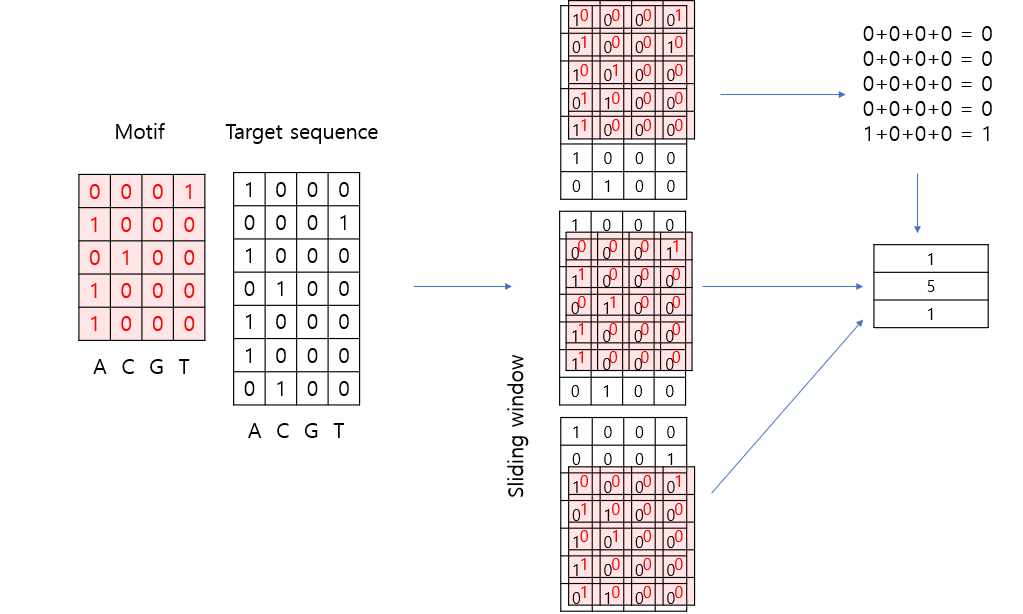
If there is a ‘5’ in the length-3 array as shown above, it indicates that the target sequence contains a sequence matching the motif.
To search for the presence of the PWM motif in the sequence “ATACAA,” a sliding window of length 5 can be used to divide the sequence into two sub-sequences: “ATACA” and “TACAA.”
- By converting these two sub-sequences into one-hot encoding and multiplying their elements with the corresponding elements of the PWM, only the PWM values at the non-zero positions of the one-hot encoding remain.
- To quantify how similar a given sequence is to the motif: 1. Multiply all non-zero values from the PWM. 2. Take the logarithm of the result.
- The resulting scalar value indicates the similarity between the sequence and the motif. Theoretically, a value of 0 implies an identical sequence match to the motif.
pwm_arr = np.array(list(pwm.values())).transpose()
print(pwm_arr.shape)
print(onehot_encode.shape)
print(onehot_encode[0:5,].shape)
print(onehot_encode[1:6,].shape)
s1 = np.multiply(onehot_encode[0:5,], pwm_arr)
s2 = np.multiply(onehot_encode[1:6,], pwm_arr)
print(s1)
print(s2)
print(np.sum(s1, axis=1))
print(np.prod(np.sum(s1, axis=1)))
print(np.log(np.prod(np.sum(s1, axis=1)))) #s1 score
print(np.log(np.prod(np.sum(s2, axis=1)))) #s2 score(5, 4)
(6, 4)
(5, 4)
(5, 4)
[[0.1 0. 0. 0. ]
[0. 0. 0. 0.1]
[0.1 0. 0. 0. ]
[0. 0.1 0. 0. ]
[0.7 0. 0. 0. ]]
[[0. 0. 0. 0.7]
[0.7 0. 0. 0. ]
[0. 0.7 0. 0. ]
[0.5 0. 0. 0. ]
[0.7 0. 0. 0. ]]
[0.1 0.1 0.1 0.1 0.7]
7.000000000000002e-05
-9.567015315914915
-2.119846956314875- Deep learning styled array
4.2.3 Simulation data generation
Generate 1,000 simulated positive sequences by embedding a motif in the middle of the sequences, and 1,000 negative sequences with random DNA sequences.
import numpy as np
seq_length = 20
num_sample = 1000
#motif CCGGAA
motif_pwm = np.array([[10.41, 22.86, 1.92, 1.55, 98.60, 86.66],
[68.20, 65.25, 0.50, 0.35, 0.25, 2.57],
[17.27, 8.30, 94.77, 97.32, 0.87, 0.00],
[4.13, 3.59, 2.81, 0.78, 0.28, 10.77]])
pwm = np.hstack([np.ones((4, 7)), motif_pwm, np.ones((4, 7))])
pos = np.array([np.random.choice( ['A', 'C', 'G', 'T'], num_sample,
p=pwm[:,i]/sum(pwm[:,i])) for i in range(seq_length)]).transpose()
neg = np.array([np.random.choice( ['A', 'C', 'G', 'T'], num_sample,
p=np.array([1,1,1,1])/4) for i in range(seq_length)]).transpose()
print(pos.shape)
display([''.join(x) for x in pos[1:5,]])
print()
display([''.join(x) for x in neg[1:5,]])(1000, 20)
['GGATTAAACGGAAACTATTT',
'AAGACTGCCGGATGGGCTCG',
'CCCGAAGGCGGAAACAATCT',
'ATGGAAGCGGGAAATATTCT']['CTACCCTTACTCGCAGGGAA',
'ACTCACTAATTGGATTGAGA',
'AGGTACCTCGCGGCATCTGG',
'GGTATCTACGTGAAGAAGGG']4.2.4 DNA data preprocessing
base_dict = {'A':0, 'C':1, 'G':2, 'T':3}
# response variable for pos
onehot_encode_pos = np.zeros((num_sample, seq_length, 4))
onehot_encode_pos_label = np.zeros((num_sample, 2), dtype=int)
onehot_encode_pos_label[:,0] = 1
# print(onehot_encode_pos_label)
# response variable for pos
onehot_encode_neg = np.zeros((num_sample, seq_length, 4))
onehot_encode_neg_label = np.zeros((num_sample, 2), dtype=int)
onehot_encode_neg_label[:,1] = 1
# print(onehot_encode_neg_label)
# convert sequence to onehot
for i in range(num_sample):
for j in range(seq_length):
onehot_encode_pos[i,j,base_dict[pos[i,j]]] = 1
onehot_encode_neg[i,j,base_dict[neg[i,j]]] = 1
# concatenation
X = np.vstack((onehot_encode_pos, onehot_encode_neg))
y = np.vstack((onehot_encode_pos_label, onehot_encode_neg_label))
print(X.shape, y.shape)
# (2000, 20, 4) (2000, 2)(2000, 20, 4) (2000, 2)- PyTorch Conv1d requires [batch_size, channels, length] so transpose(1,2) excuted
import torch
from torch.utils.data import TensorDataset, DataLoader
from sklearn.model_selection import train_test_split
# 데이터를 훈련 세트와 테스트 세트로 나눔
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=125)
print(X_train.shape, y_train.shape)
# NumPy 배열을 PyTorch 텐서로 변환
X_train = torch.tensor(X_train, dtype=torch.float32).transpose(1,2)
X_test = torch.tensor(X_test, dtype=torch.float32).transpose(1,2)
y_train = torch.tensor(y_train, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)
print(y_test.dtype)
# DataLoader 설정
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
print(train_loader.dataset.tensors[0].shape)
print(train_loader.dataset.tensors[1].shape)
test_dataset = TensorDataset(X_test, y_test)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)(1600, 20, 4) (1600, 2)
torch.float32
torch.Size([1600, 4, 20])
torch.Size([1600, 2])import torch
X_torch = torch.tensor(X_train, dtype=torch.float32)
print(X_torch.shape)torch.Size([1600, 4, 20])/tmp/ipykernel_2688/3124571761.py:3: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).
X_torch = torch.tensor(X_train, dtype=torch.float32)4.3 CNN model
import torch.nn as nn
import torch.optim as optim
import torch
import torch.nn as nn
import torch.optim as optim
class DNA_CNN(nn.Module):
def __init__(self):
super(DNA_CNN, self).__init__()
self.conv1 = nn.Conv1d(in_channels=4, out_channels=16, kernel_size=3, padding=1)
self.relu = nn.ReLU()
self.maxpool = nn.MaxPool1d(kernel_size=2)
self.flatten = nn.Flatten()
self.fc1 = nn.Linear(160, 64) # Adjust the input features according to your pooling and conv1d output
self.fc2 = nn.Linear(64, 2) # Adjust according to your problem's needs (e.g., number of classes)
#self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.conv1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.flatten(x)
x = self.fc1(x)
x = self.fc2(x)
#x = self.softmax(x)
return x
model = DNA_CNN()
if torch.cuda.is_available():
model.cuda()
# Loss and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
from torchsummary import summary
summary(model, input_size=(4, 20)) # (Channels, Length)----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv1d-1 [-1, 16, 20] 208
ReLU-2 [-1, 16, 20] 0
MaxPool1d-3 [-1, 16, 10] 0
Flatten-4 [-1, 160] 0
Linear-5 [-1, 64] 10,304
Linear-6 [-1, 2] 130
================================================================
Total params: 10,642
Trainable params: 10,642
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.04
Estimated Total Size (MB): 0.05
----------------------------------------------------------------4.3.1 Training
# 훈련 루프
num_epochs = 20
for epoch in range(num_epochs):
for inputs, labels in train_loader:
if torch.cuda.is_available():
inputs, labels = inputs.cuda(), labels.cuda()
# Forward pass
outputs = model(inputs)
loss = criterion(outputs, labels)
# Backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')
Epoch [1/20], Loss: 0.5050
Epoch [2/20], Loss: 0.2472
Epoch [3/20], Loss: 0.1437
Epoch [4/20], Loss: 0.0821
Epoch [5/20], Loss: 0.0966
Epoch [6/20], Loss: 0.0719
Epoch [7/20], Loss: 0.0729
Epoch [8/20], Loss: 0.0387
Epoch [9/20], Loss: 0.1018
Epoch [10/20], Loss: 0.1520
Epoch [11/20], Loss: 0.0712
Epoch [12/20], Loss: 0.0277
Epoch [13/20], Loss: 0.0272
Epoch [14/20], Loss: 0.0318
Epoch [15/20], Loss: 0.0215
Epoch [16/20], Loss: 0.0464
Epoch [17/20], Loss: 0.0975
Epoch [18/20], Loss: 0.0566
Epoch [19/20], Loss: 0.0191
Epoch [20/20], Loss: 0.05164.3.2 Model evaluation
# 모델 평가
model.eval()
with torch.no_grad():
correct = 0
total = 0
for inputs, labels in test_loader:
if torch.cuda.is_available():
inputs, labels = inputs.cuda(), labels.cuda()
outputs = model(inputs)
#print(outputs.data)
_, predicted = torch.max(outputs.data, 1)
#print(predicted)
total += labels.size(0)
labels_max = torch.max(labels, 1)[1]
#print(labels_max)
correct += (predicted == labels_max).sum().item()
print(f'Accuracy of the model on the test images: {100 * correct / total} %')Accuracy of the model on the test images: 98.5 %4.4 Training and evaluation
import matplotlib.pyplot as plt
# 데이터 저장을 위한 리스트 초기화
train_losses = []
val_accuracies = []
num_epochs = 200
for epoch in range(num_epochs):
model.train()
running_loss = 0.0
for inputs, labels in train_loader:
if torch.cuda.is_available():
inputs, labels = inputs.cuda(), labels.cuda()
# Forward pass
outputs = model(inputs)
loss = criterion(outputs, labels)
# Backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item() * inputs.size(0)
epoch_loss = running_loss / len(train_loader.dataset)
train_losses.append(epoch_loss)
# 모델 평가
model.eval()
correct = 0
total = 0
with torch.no_grad():
for inputs, labels in test_loader:
if torch.cuda.is_available():
inputs, labels = inputs.cuda(), labels.cuda()
outputs = model(inputs)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
labels_max = torch.max(labels, 1)[1]
correct += (predicted == labels_max).sum().item()
epoch_accuracy = 100 * correct / total
val_accuracies.append(epoch_accuracy)
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {epoch_loss:.4f}, Accuracy: {epoch_accuracy:.2f}%')
# 그래프 그리기
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Training Loss')
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(val_accuracies, label='Validation Accuracy')
plt.title('Validation Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy (%)')
plt.legend()
plt.show()NameError: name 'model' is not defined