Chapter 7 Statistical inference

7.1 Introduction

통계적 추정이란 모집단으로부터 임의 추출된 표본을 이용하여 모집단을 추정하는 과정을 의미합니다. 앞에서 배운 내용이지만 다음 네 가지 중요한 키워드들이 있습니다.

모집단 (population)
모수 (Parameter) - 모집단의 분포를 설명하는 특정 값
표본 (sample) - 모집단으로부터 임의 추출된 관측값의 모음
통계량 (statistics) - 표본의 평균, 분산과 같은 대표값

다음은 표준정규분포 모집단에서 (모수: \(\mu, \sigma\)) 16개 표본을 임의 추출하여 평균을 (통계량) \(\bar{x}\) 구하고 이 과정을 10번 반복한 상황을 표현한 그림으로 통계적 추론의 과정을 보여 줍니다.

[UsingR for introductory statistics, 243 페이지]

어떤 임의 표본에 대해서 \(\bar{x}\)의 표본분포는 \(\mu\) 근처에 위치
어떤 임의 표본에 대해서 \(\bar{x}\)의 표본분포의 표준편차는 \(\sigma/\sqrt{n}\) 로 표현 (\(\sigma\)는 모분산, 표본들의 분산보다 작음)
모분포가 정규분포이면 \(\bar{x}\)도 정규분포 (반복이 많아질수록, 중심극한정리)
시뮬레이션으로 이론 확인

7.2 Simulation

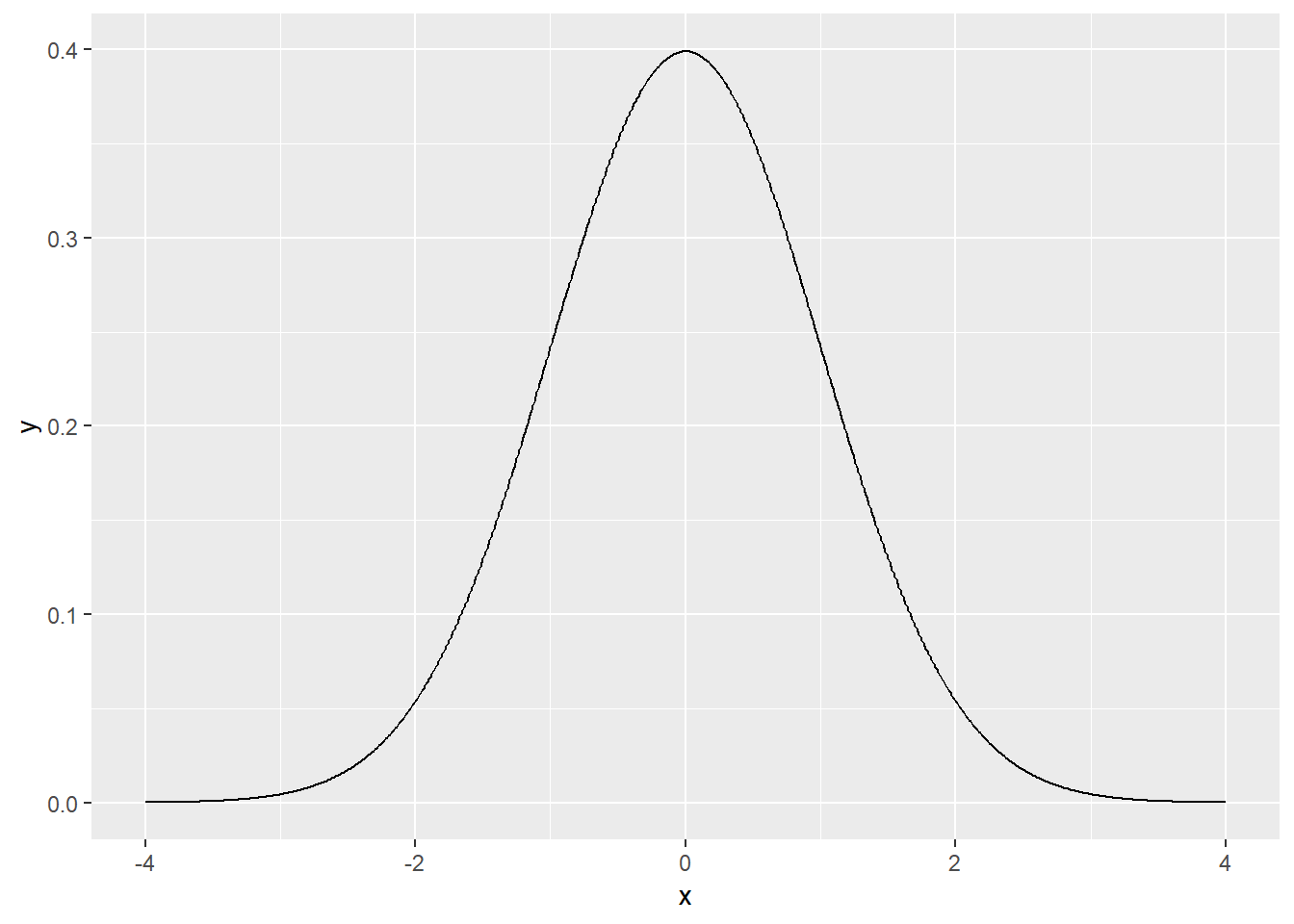
[EXERCISE] N(0, 1)의 분포를 dnorm을 이용해 그리시오 (xlim=c(-4,4))

[EXERCISE] 표준정규분포로부터 16개의 표본을 뽑아 평균을 구하고 각 표본과 평균 값들을 y=1 위치에 점으로 표현하시오 (rnorm사용)

[EXERCISE] 위 예제를 두 번 반복하되 두 번째 데이터는 y=0.9 위치에 표현하시오

library(ggplot2, quietly = T)

nsample <- 16
x <- rnorm(nsample*2, 0, 1)
y <- c(rep(1, nsample), rep(0.9, nsample))
g <- factor(c(rep(1, nsample), rep(2, nsample)))

dat <- data.frame(x, y, g)

ggplot(dat, aes(x, y)) +
  geom_point() +
  geom_point(aes(x=mean(x[1:nsample]), y=1), colour="blue", size=5, shape=15) +
  geom_point(aes(x=mean(x[(nsample+1):length(x)]), y=0.9), colour="blue", size=5, shape=15) +
  scale_y_continuous(limits=c(0, 1.2))

[EXERCISE] 위 예제를 10번 반복하되 각 반복 데이터는 각각 y=1, 0.9, 0.8, …, 0.1 위치에 표현하시오

suppressWarnings(suppressMessages(library(ggplot2, quietly = T)))
suppressWarnings(suppressMessages(library(dplyr, quietly = T)))

nsample <- 16
nrep <- 10

x <- rnorm(nsample*nrep, 0, 1)
tmpy <- seq(0.1, 1, length.out=nrep)
y <- rep(tmpy, each=nsample)
## ?rep
g <- factor(y)

dat <- data.frame(x, y, g)
dat_mean <- dat %>% 
  group_by(g) %>% 
  summarise(mean=mean(x))

ggplot(dat, aes(x, y)) +
  geom_point() +
  scale_y_continuous(limits=c(0, 1.1)) +
  geom_point(data=dat_mean, aes(y=as.numeric(as.character(g)), x=mean), colour="blue", size=5, shape=15)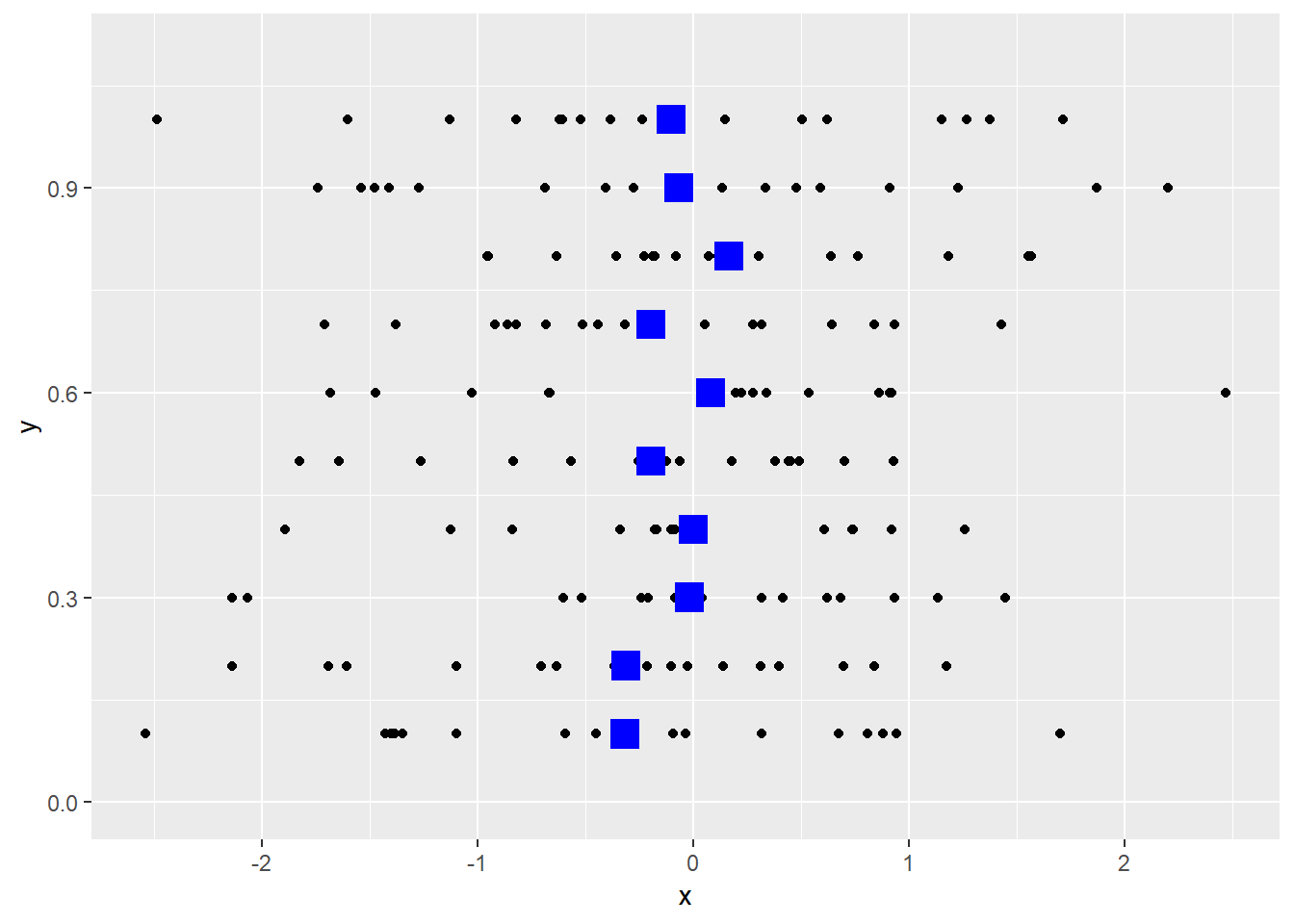

str(dat_mean)

## Classes 'tbl_df', 'tbl' and 'data.frame':    10 obs. of  2 variables:
##  $ g   : Factor w/ 10 levels "0.1","0.2","0.3",..: 1 2 3 4 5 6 7 8 9 10
##  $ mean: num  -0.317073 -0.314665 -0.018363 0.000455 -0.1986 ...

as.numeric(as.character(dat_mean$g))

##  [1] 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

ggplot() + 
  geom_point(data=dat, aes(x, y)) +
  geom_point(data=dat_mean, aes(x=mean, y=as.numeric(as.character(dat_mean$g))), colour="blue", size=5, shape=15) +
  theme_bw()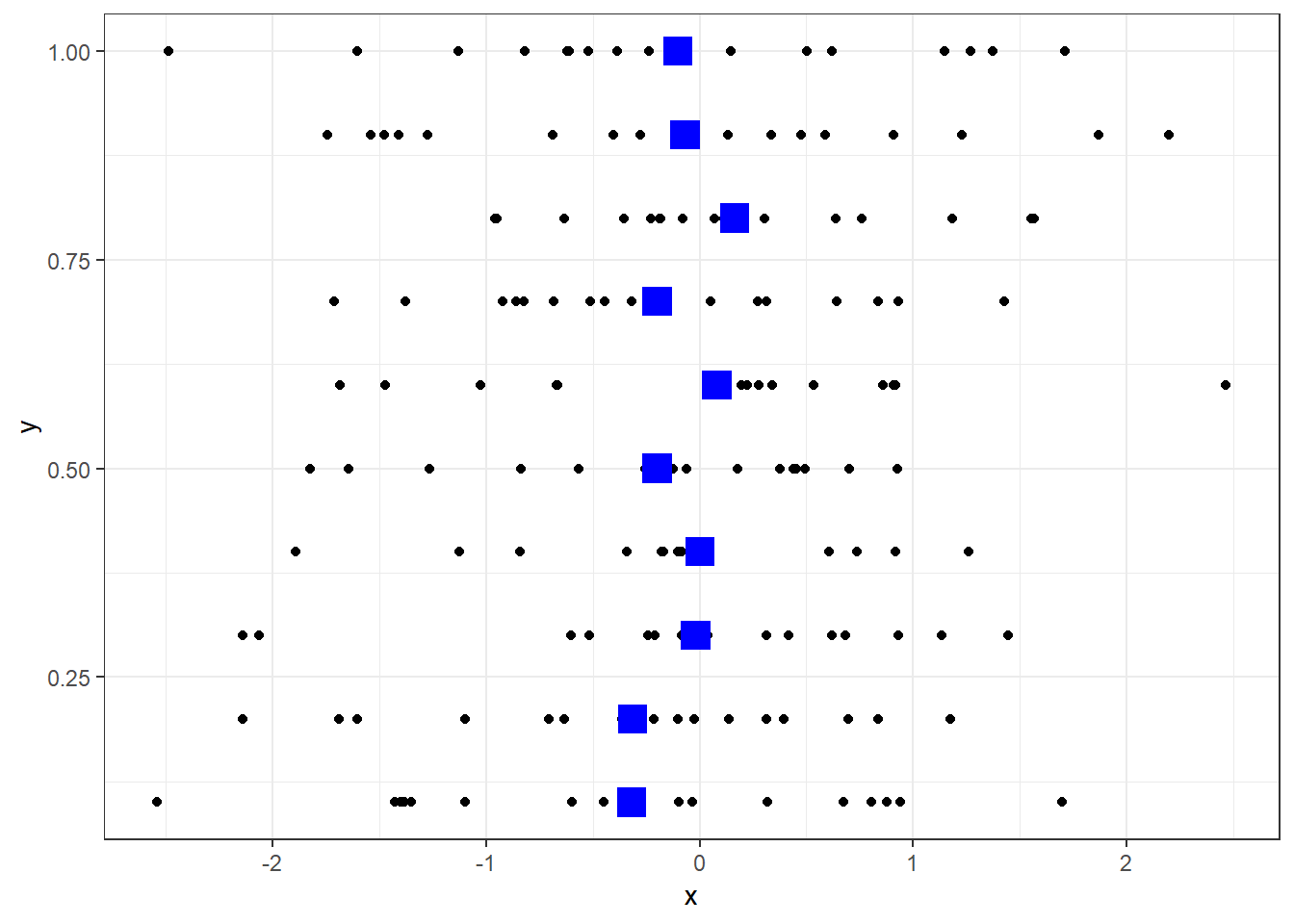

[EXERCISE] 위 예제와 함께 표준정규분포 곡선과 \(\bar{x}\)의 분포를 모두 같이 그리시오

7.3 Significance tests

두 그룹의 데이터 (표본)을 가지고 있을 때 두 그룹이 통계적으로 차이가 있는지를 검증하는 방법으로 (코흐트 데이터, Case-control 데이터) 시뮬레이션에 의한 방법을 먼저 소개하고 이 후 분포를 기준으로 통계적 검증을 알아보겠습니다.

카페인(커피)이 초초한 상태를 유발하는가? 라는 질문에 답하기 위해서 보통 두 그룹의 평균의 차이를 비교합니다.

coff <- c(245, 246, 246, 248, 248, 248, 250, 250, 250, 252)
nocoff <- c(242, 242, 242, 244, 244, 245, 246, 247, 248, 248)
dat <- data.frame(coff, nocoff)
obs <- with(dat, mean(coff) - mean(nocoff))
obs

## [1] 3.5

Randomization distribution 상태로 데이터를 다시 두 그룹으로 나누어 차이를 계산하고 이 과정을 반복해서 분포를 그려보겠습니다.

[EXERCISE] 두 그룹 데이터에서 임으로 10명을 두 번 뽑아 그 평균의 차이를 계산하시오

## [1] -1.1

[EXERCISE] 위 예제의 과정을 1000번 반복하고 각 차이값의 분포를 그리시오

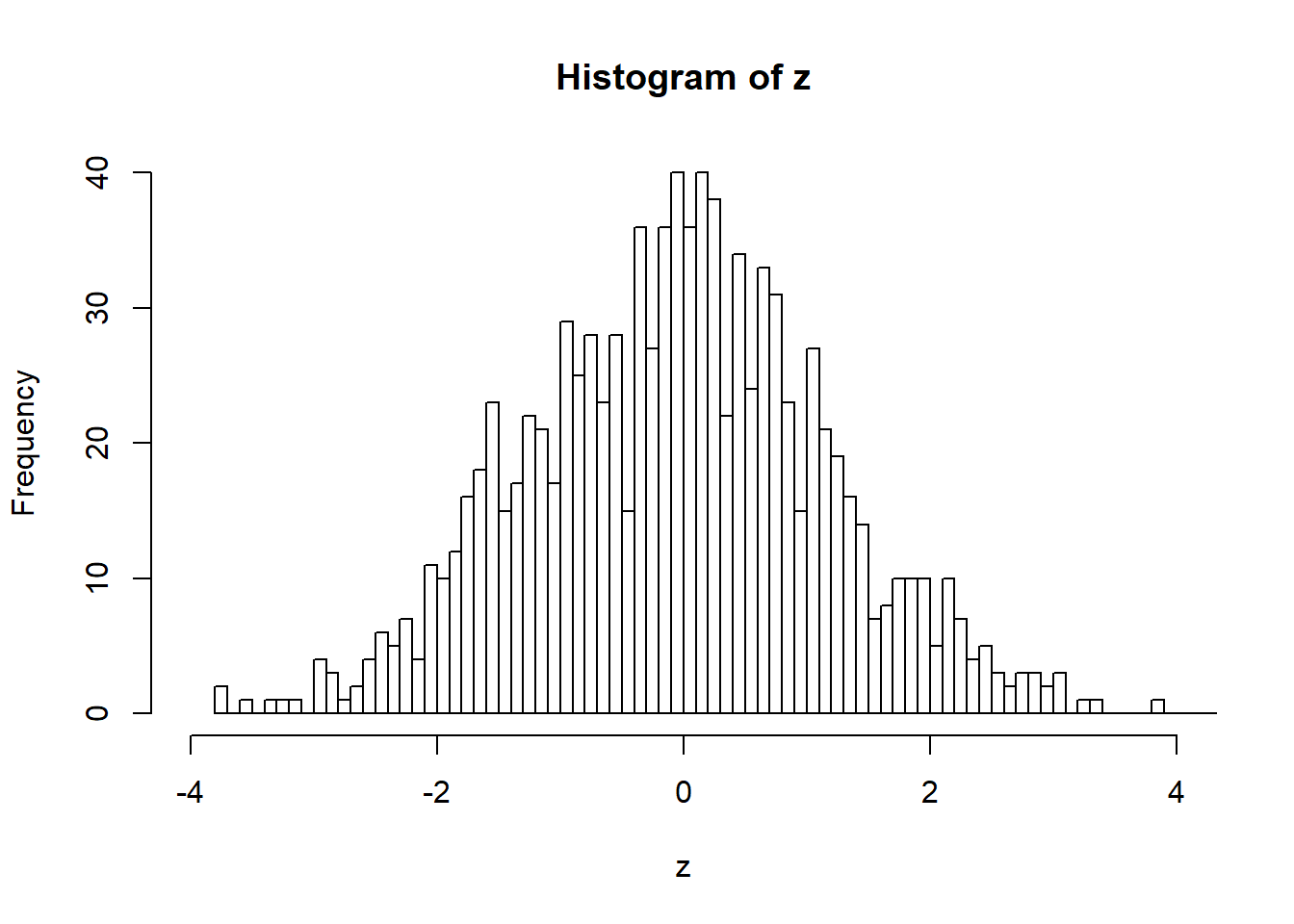
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.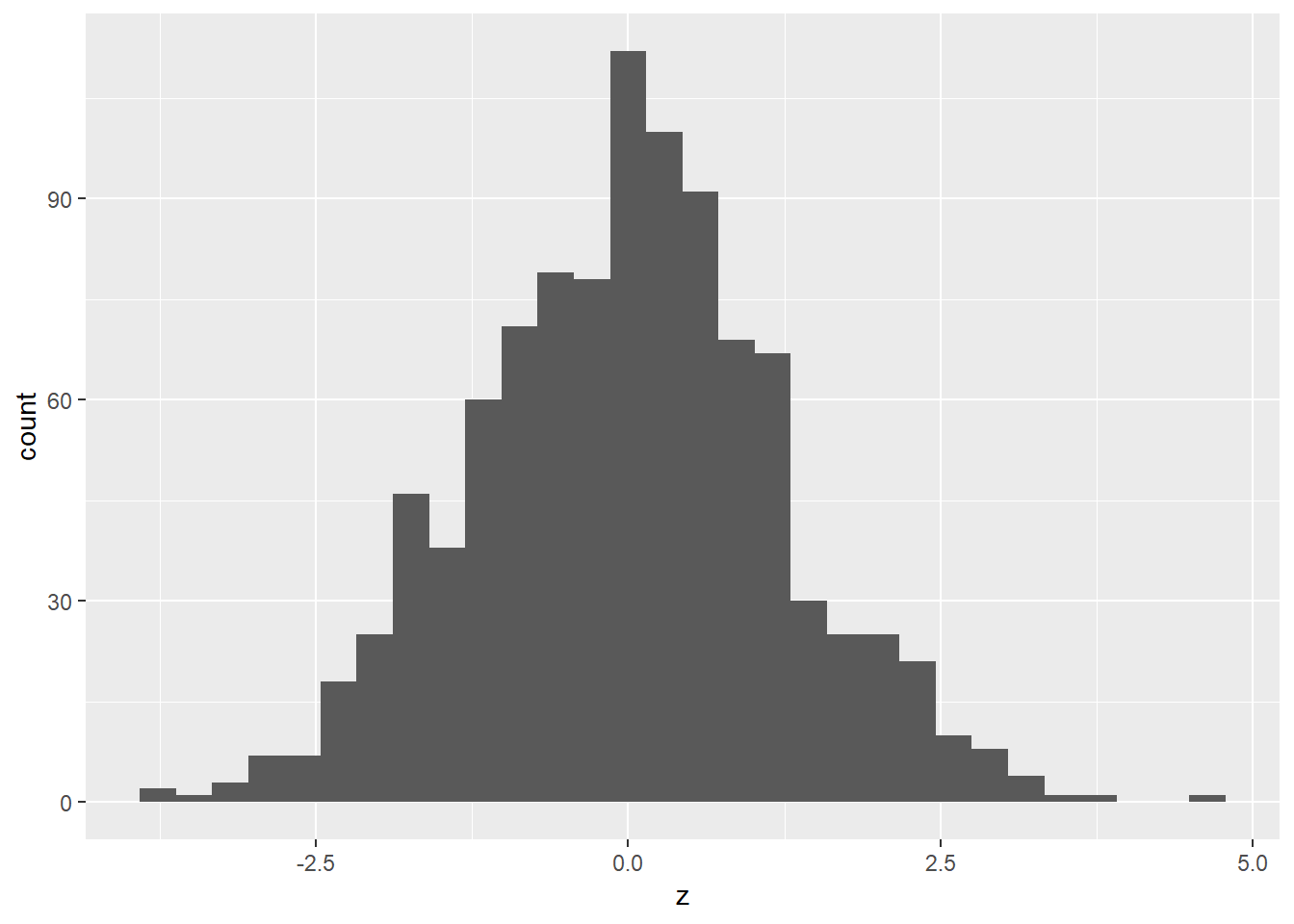

[EXERCISE] 분포에서 실제 관측한 3.5 값의 위치를 표시하고 관측값보다 더 극단적인 경우가 나올 경우의 비율을 계산하시오

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.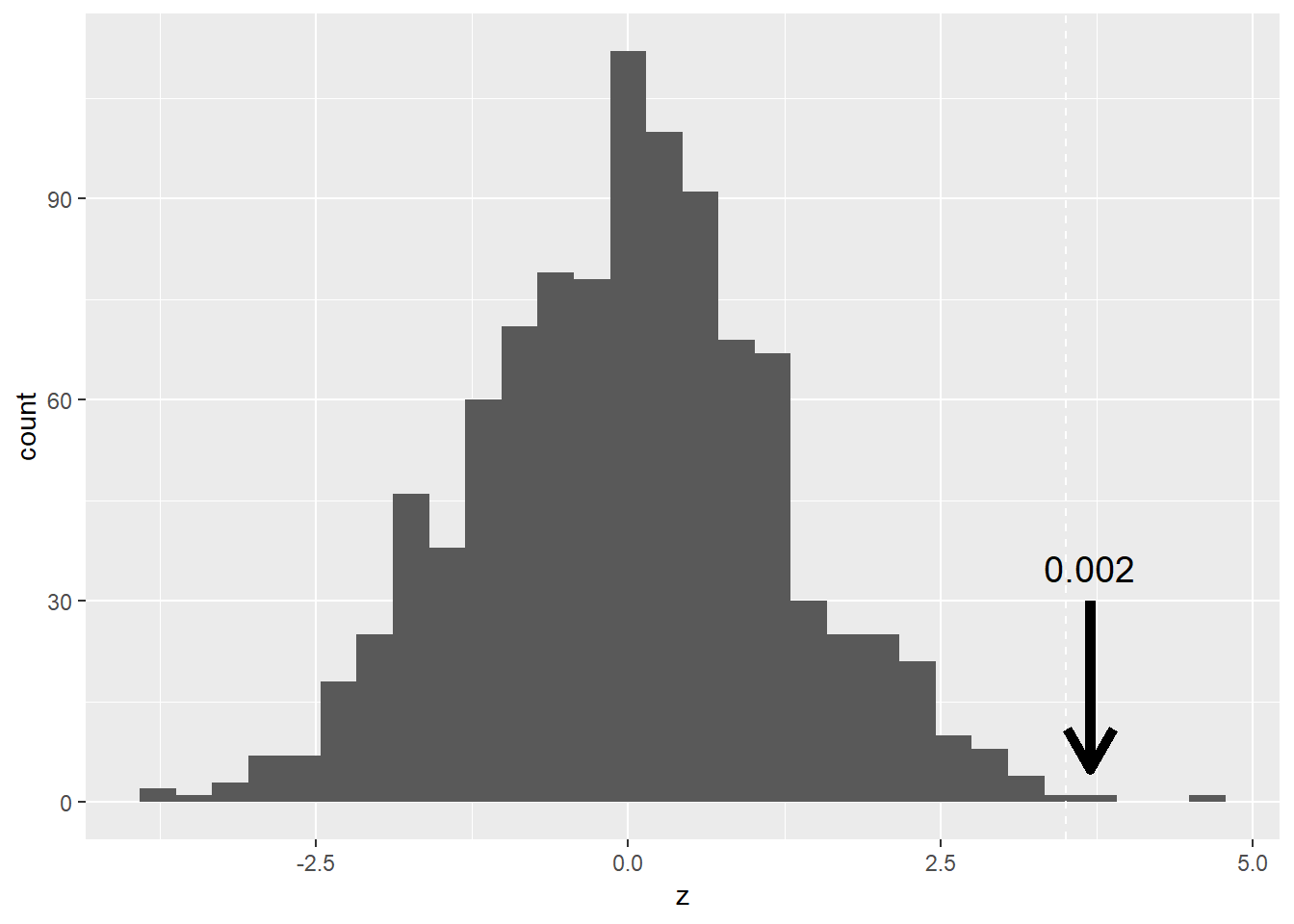

7.4 Estimation and confidence interval

앞서 예제에서 두 그룹간 평균의 차이가 통계량 (statistic) 입니다. 통계량은 모수 (parameter)를 추정하기 위한 값으로 볼 수 있고 이 값이 얼마나 모수와 가까운지, 즉 차이가 0에 가까운지 판단하는 것은 통계적 추정에서 가장 중요한 부분 중 하나 입니다. 일반적으로 \(\mu, \sigma\) 등 모수는 \(\theta\)로 표현하고 \(\theta\)를 추정하기위한 통계량은 \(\hat{\theta}\)로 표현합니다. 다음 식으로 우리가 계산한 통계량이 얼마나 모수에 가까운지는 다음 식으로 알 수 있습니다.

\[ E((\hat{\theta} - \theta)^2) = VAR(\hat{\theta}) + (E(\hat{\theta}-\theta))^2 = \text{variance} + \text{bias}^2 \] 우리가 언급하는 통계량들은 대부분 unbiased 입니다. 불편추정량 (unbiased estimator)이라 부르며 다음과 같은 것들이 있습니다.

\(E(\bar{x}) = \mu\)
\(E(\bar{p}) = p\)
\(E(s^2) = \sigma^2\)

예를 들어 A poll asking a random sample of 1003 whether marriages between same-sex couples should be recognized by law as valid. 55% said yes, 이 경우 A randomly selected person would responding yes with \(\hat{p}\) = 0.55 입니다.

여기서 이러한 투표를 100번 반복 했을 때 계산되는 찬성 비율 값들이 대부분 (또는 95%는) 어디에 모여 있는가? 라는 질문을 할 수 있고 이는 모집단에서의 찬성 비율 (모수, 진짜) 값의 95% 신뢰구간은 무엇인가? 라는 질문과 같습니다. 이를 위해 다음 시뮬레이션을 수행할 수 있습니다.

p <- 0.55
n <- 1003
x <- rbinom(1000, n, p)
#mean(x)
hist(x, br=100)

quantile(x, c(0.025, 0.975))

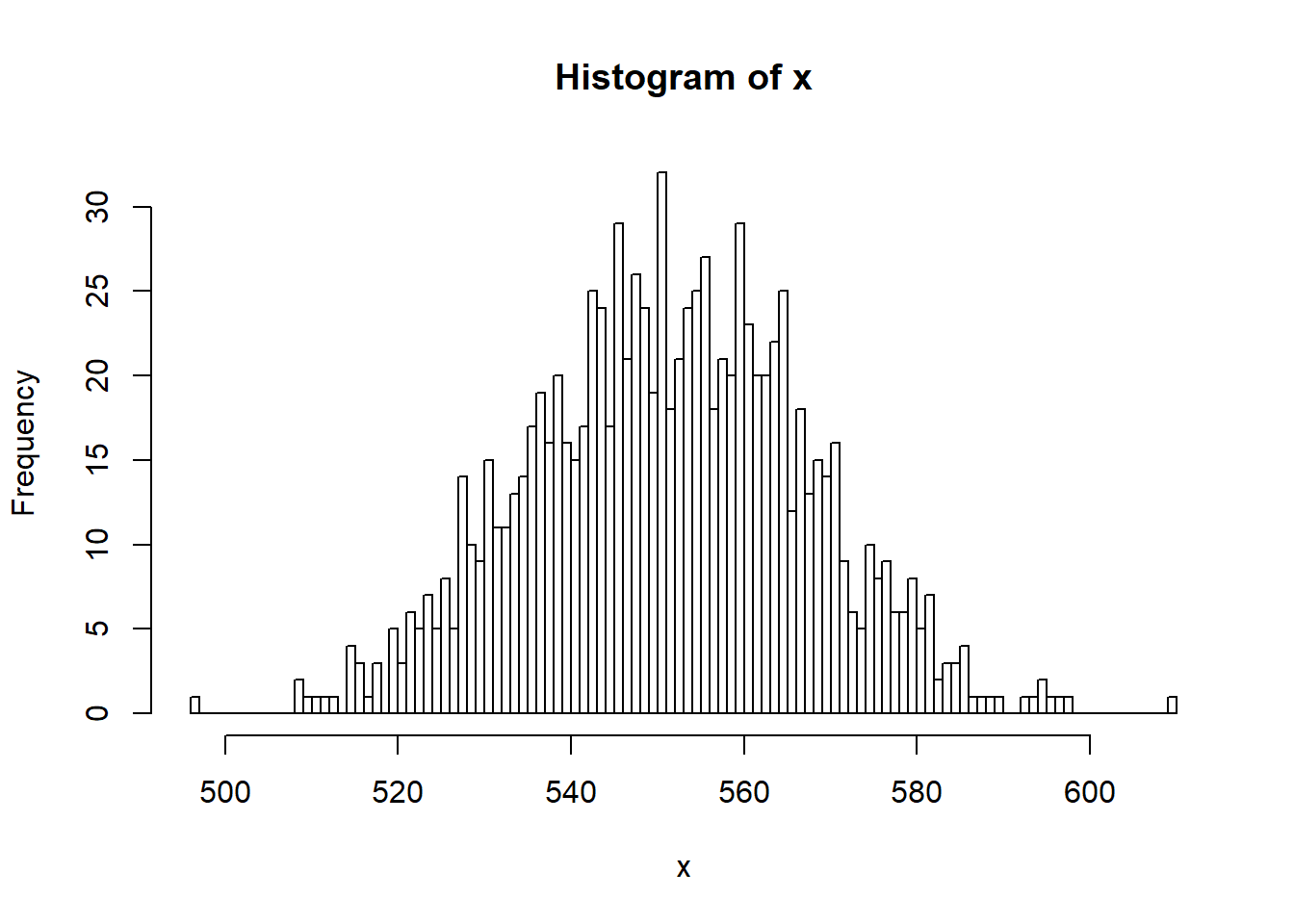
##  2.5% 97.5% 
##   521   582

앞 뒤 0.025%를 제외한 구간은 위와 같으며 위 구간이 95% 신뢰구간이 됩니다. 뒤에서 설명이 나오지만 여기서 신뢰구간의 해석을 한 번 생각해 보면 좋습니다.

그런데 현실에서는 1000번의 반복이 불가능하며 1번 또는 2번의 데이터로 95% 신뢰구간을 구해야 합니다. 즉, 위 예제에서 1003명에 대한 설문조사로 \(\hat{p}=0.55\) 가 나왔다는 정보 하나만으로 신뢰구간을 추정해야 하는 것 입니다.

여기서 다시 기억할 부분은 앞에서 배운 확률변수 표본평균의 표본 분포는 정규분포이며 그 표준편차는 모표준편차를 \(\sqrt{n}\)으로 나누어준 값이라는 것 입니다. (후에 좀 더 학습할 예정이며 지금은 시뮬레이션으로 얼마든지 반복해서 샘플링이 가능한 것으로 생각하겠습니다) 결국 데이터는 하나뿐이지만 분포를 정규분포로 알고 있으므로 신뢰구간도 구할 수 있는 것 입니다. 좀 더 명확한 분포를 정보를 위해 표준정규분포로 전환하며 표준정규분포를 따르는 z-통계량은 다음과 같이 나타낼 수 있습니다.

\[ \hat{p} = p \to \hat{p} - p =0 \\ z = \frac{\hat{p} - p}{SD(\hat{p})} \sim N(0,1) \]

그런데 \(SD(\hat{p})=\sigma/\sqrt{n}\)는 알 수 없으므로 중심극한정리에 의해 \(n\)이 충분히 클 경우 \(SD(\hat{p})\)의 모표준편차 \(\sigma\)를 샘플의 표준편차로 대체한 표준오차 \(SE(\hat{p})=s/\sqrt{n}\)를 사용합니다. 베르누이 분포에서 샘플의 표준편차\(s\)는 \(\sqrt{\hat{p}(1-\hat{p})}\) 이므로 \(SE(\hat{p})=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\) 입니다.

이제 위 투표 예제의 \(\hat{p}=0.55\)와 \(n=1003\)을 위 z값 공식에 대입해 봅니다.

\[ z = \frac{0.55 - p}{0.0157} \]

그런데 \(p\)값은 우리가 관심있는 모수이고 z 값은 표준정규분포 이므로 아래 z 값의 특정 범위를 지정할 수 있습니다. 결국 \(p\) 값만 남기고 모든 항을 넘기면 \(p\)값의 범위를 구할 수 있습니다. 후에 이러한 방법으로 신뢰구간을 구하는 방법을 알아봅니다.

모평균에 대한 신뢰구간도 유사한 방법으로 구할 수 있습니다. 평균 100, 표준편차 16인 모분포에서 4개의 샘플을 랜덤하게 추출하여 그 평균을 구하는 시뮬레이션을 수행합니다. 확률변수 평균의 \(\bar{x}\) 분포는 정규분포를 따르고 표준화 값인 z값은 표준정규분포 N(0, 1)을 따릅니다. 다음과 같은 시뮬레이션으로 확인할 수 있으며 95% 신뢰구간도 quantile함수를 이용해서 구할 수 있습니다.

mu <- 100
sigma <- 16
M <- 1000
n <- 4
res <- replicate(M, {
    x <- rnorm(n, mu, sigma)
    se <- sd(x)/sqrt(n)
    (mean(x) - mu)/se
})

quantile(res, c(0.025, 0.975))

##      2.5%     97.5% 
## -2.951469  3.172565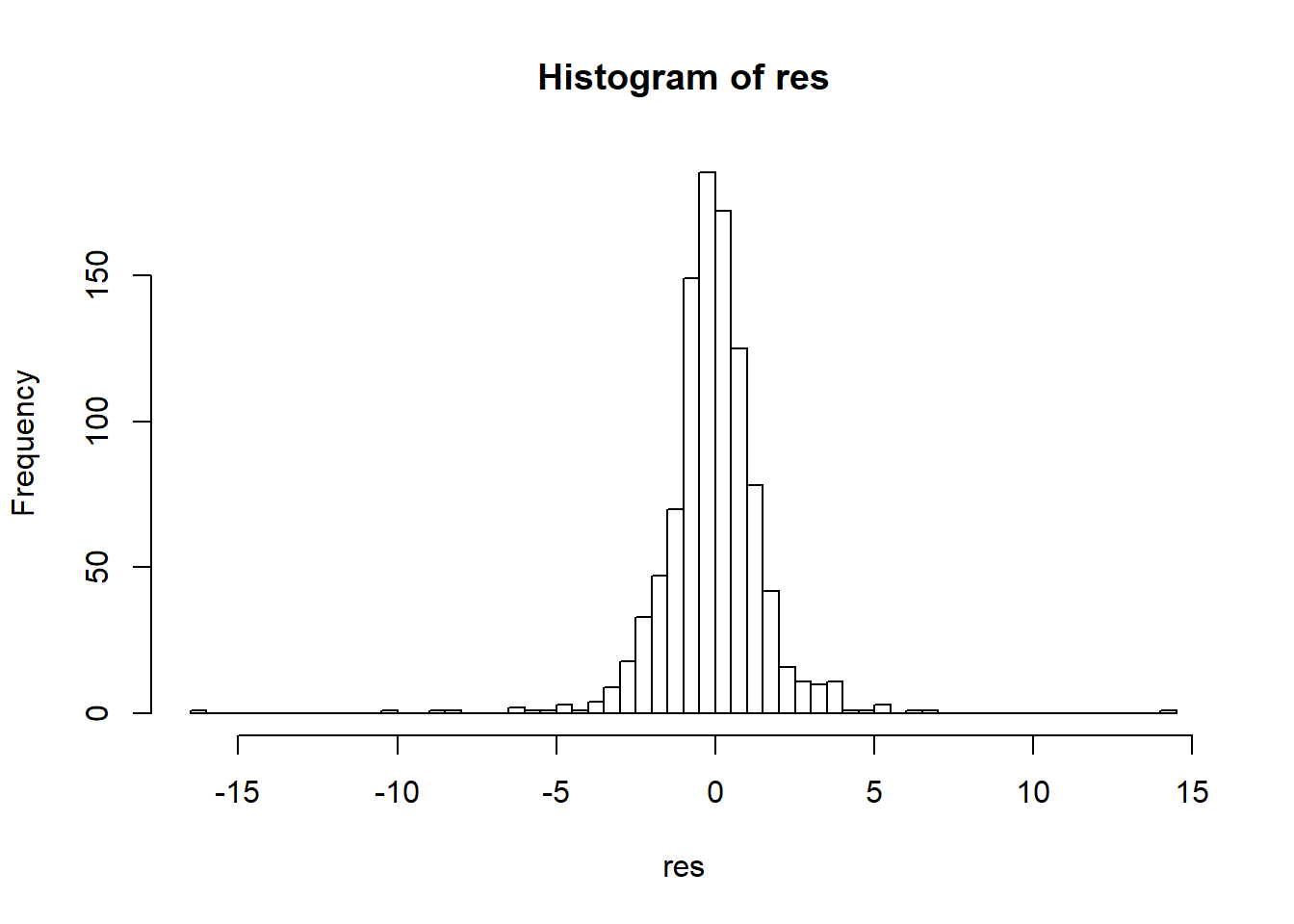

hist(res, br=100)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.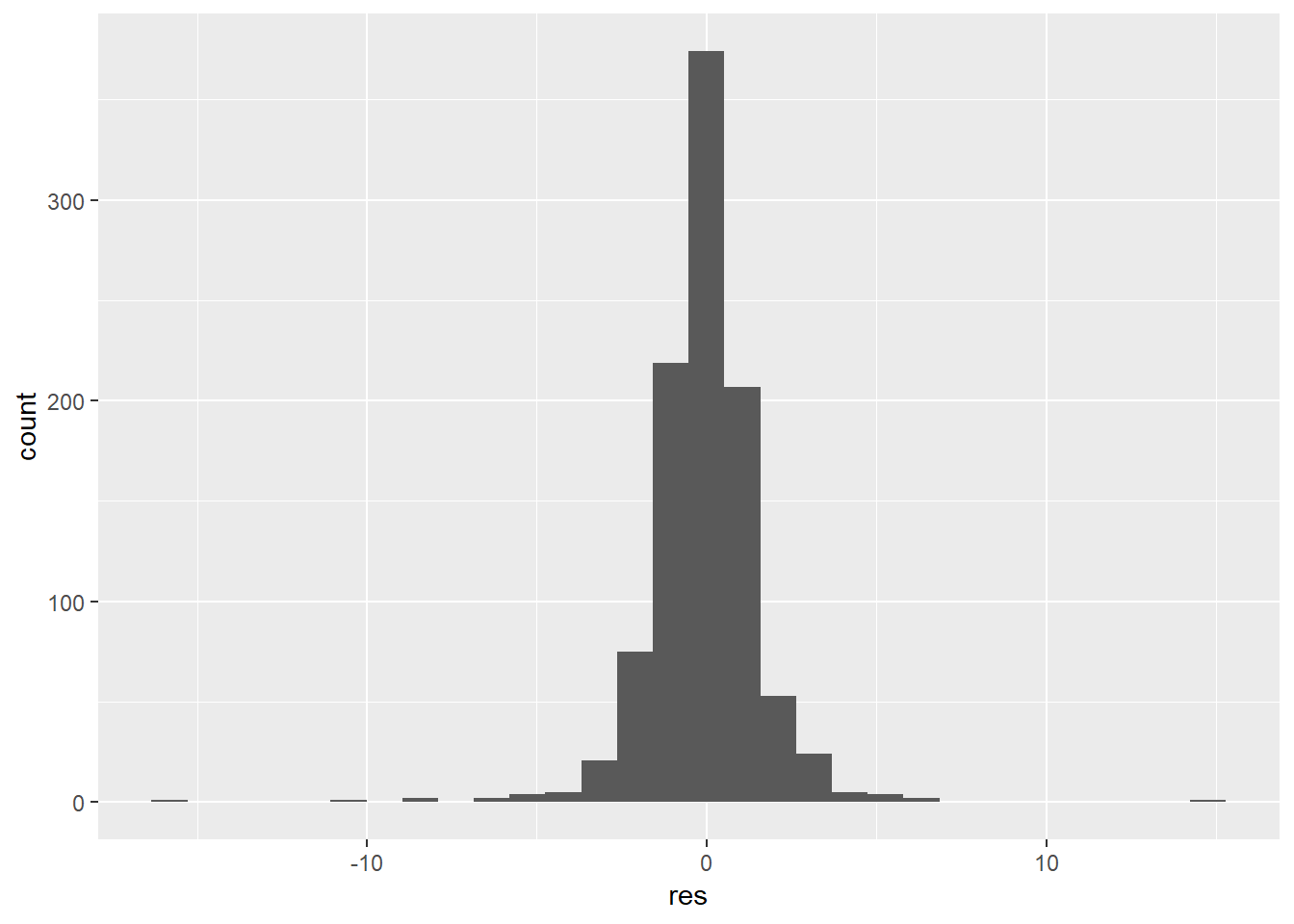

시뮬레이션을 사용할 수 없는 일반적인 경우 신뢰구간을 구하는 방법을 알아봅니다. 다음과 같이 \(\mu\)를 모평균, \(\bar{x}\)를 확률변수 t-통계량은 \(\sigma\) 대신 \(s\)를 사용한 경우를 말합니다.

\[\begin{split} \bar{x} &= \mu \to \bar{x} - \mu =0 \\ z &= \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \sim N(0,1) \\ t &= \frac{\bar{x} - \mu}{s/\sqrt{n}} \sim T \end{split}\]

참고로 다음은 오차 (error), 편차/잔차 (deviance/residual), 그리고 편향 (bias) 에대한 개념을 나타냅니다.

이제 확률변수 평균 \(\bar{x}\)의 95% 신뢰구간을 구해봅니다. 이는 앞서 언급한바와 같이 샘플링 후 평균을 구하는 과정을 계속 반복할 경우 데이터의 95% 가 어디 있는가에 대한 질문과 같으며 이는 위와 같은 대칭형 표준정규분포에서 왼쪽 0.025% 와 오른쪽 0.025%를 제외한 가운데 부분의 데이터를 말합니다.

\[ \begin{split} -3.33 < \frac{\bar{x} - \mu}{s/\sqrt{n}} < 3.07 \\ \bar{x} -3.33 \times s/\sqrt{n} < \mu &< \bar{x} + 3.07 \times s/\sqrt{4} \end{split} \]

7.5 Bootstrap

분포를 모를 경우 분포를 생성하는 방법으로 적당한 수의 샘플 수가 있을 경우에 가능한 방법입니다. UsingR 패키지의 Dedicare 데이터셋을 예로 들면, 병원비 청구 금액과 지불금액의 차이가 큰 범위의 분포를 가지고 있는 상황이며 합리적인 (?) 신뢰구간을 구하는 문제입니다.

suppressWarnings(suppressMessages(library(UsingR, quietly = T)))
suppressWarnings(suppressMessages(library(ggplot2)))
diabetes <- subset(Medicare, subset= DRG.Definition =="638 - DIABETES W CC")
gap <- with(diabetes, Average.Covered.Charges-Average.Total.Payments)
ggplot(data.frame(gap), aes(x=gap)) + geom_histogram(bins=30)

sample 함수 복원 추출 허용 분포를 생성합니다.

M <- 2000
res <- replicate(M, {
  xstar <- sample(gap, length(gap), replace=T)
  mean(xstar) - xbar
})
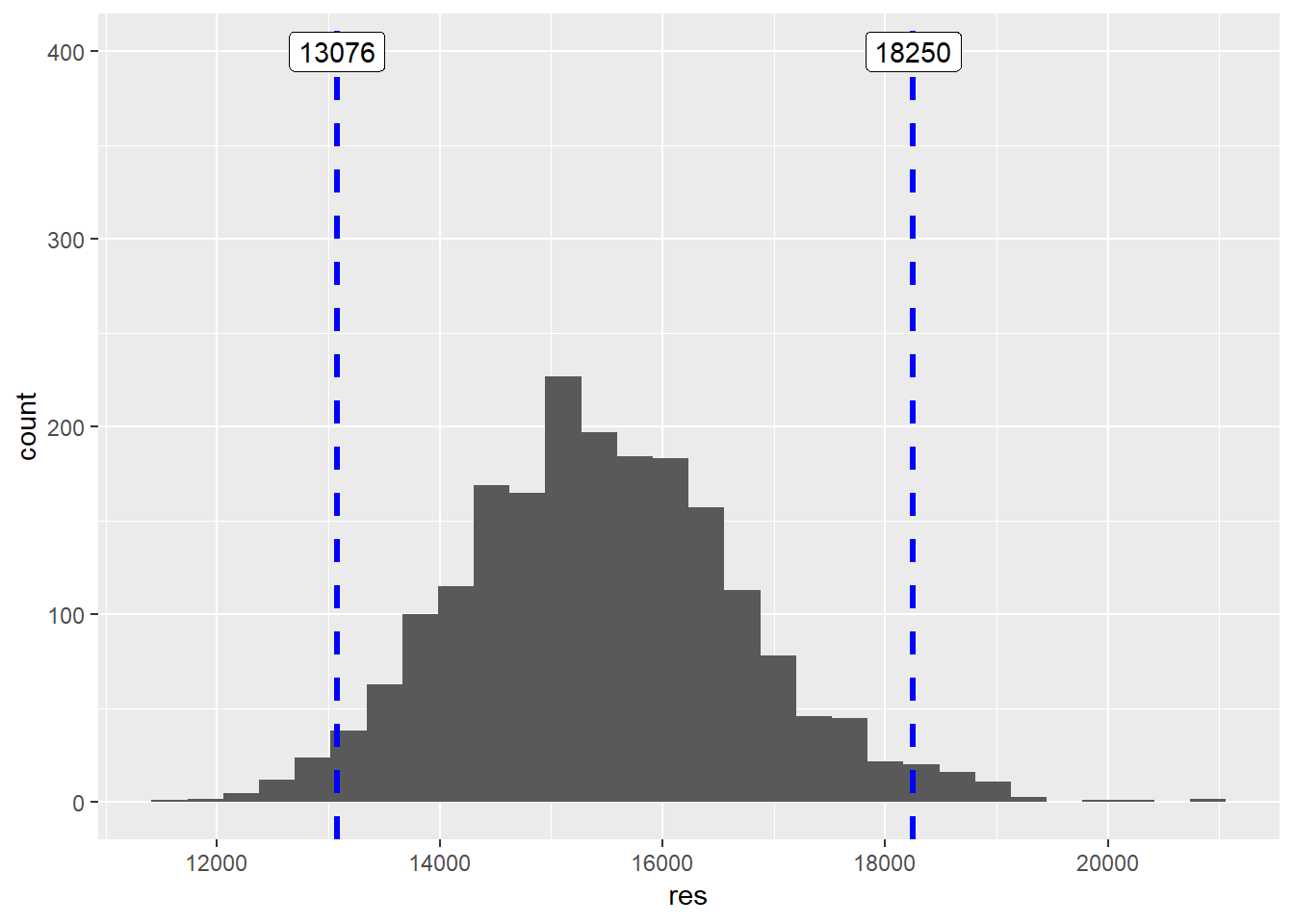
conf95 <- quantile(res, c(0.025, 0.975))
ggplot(data.frame(res), aes(x=res)) + 
  geom_histogram(bins=30) +
  geom_vline(xintercept=conf95, linetype="dashed", color='blue', size=1.2) +
  geom_label(aes(x=conf95[1], y=400, label=round(conf95[1]))) +
  geom_label(aes(x=conf95[2], y=400, label=round(conf95[2])))

R로 배우는 기초통계